Chronique raisonnable n° 18 ou leçon d’autodéfense intellectuelle du jeudi 5 avril 2012

=====================================================================
18^ème Leçon d’autodéfense intellectuelle – Jeudi 5 avril 2012

=====================================================================

 18^ème chronique raisonnable, pour :

o     apprendre à soumettre à la critique les informations reçues

·        prévenir les manipulations et

·        démonter les croyances,

« Être libre, c’est ne plus avoir peur et être responsable de sa vie ».

Continuons ensemble l’étude des pièges d’un usage malicieux des mathématiques : apprendre à compter pour ne pas s’en laisser conter. Rappelez-vous l’émission précédente !

Nous avons vu quelques-unes des outils de base de la statistique, comme la courbe de Gauss-Laplace, la courbe en chapeau, on l’appelle aussi courbe de la distribution normale, elle concerne la représentation de la distribution de nombreux phénomènes humains ou naturels. Nous avons aussi vu les notions de mesures tendancielles que sont la moyenne, la médiane ou le mode.

Pour reprendre la pertinence de bien connaître ces dernières notions, prenons l’exemple d’une entreprise XYZ dont l’objet principal est de fabriquer des Spountz. A la direction se trouvent le patron, son frère et six parents, le personnel de l’entreprise est lui composé de cinq contremaîtres et de dix ouvriers. L’entreprise se trouve dans une phase ascendante de son activité et est amenée à embaucher un nouvel employé. Paul est candidat au poste. Le patron de XYZ lui explique que le salaire moyen dans l’entreprise est de 6000 € par mois. Il précise qu’au début, il sera embauché avec un salaire de 1500 € par mois pendant la période d’essai, et qu’ensuite son salaire augmentera vite.

Paul est embauché, mais après quelques jours et avoir discuté avec ses collègues, il est très en colère et va voir son employeur en lui disant qu’il lui a menti, car aucun ouvrier de XYZ ne touche plus de 2000 € par mois.

L’employeur rétorque en lui montrant tous les salaires versés par l’entreprise XYZ chaque mois :

Patron : 48000 €

Son frère : 20000 €

Chacun des six parents : 5000 €

Chacun des cinq contremaîtres : 4000 €

Chacun des dix employés : 2000€

Au total, l’entreprise XYZ paie 138000 € par mois en salaires à 23 personnes, le salaire moyen est donc bien de 138000 € / 23 = 6000 €.

Il conclut : « Vous voyez bien que je ne vous ai pas menti »

Mais Paul en penseur critique ayant écouté notre précédente émission, lui rétorque : « la moyenne que vous utilisez est une mesure de tendance centrale. Il y en a d’autres, vous auriez été plus honnête en me donnant la médiane. Dans ce cas, le salaire médian de XYZ est de 4000 €, cela m’aurait plus éclairé. Mais pour être tout à fait honnête, vous auriez pu me donner le mode qui est le nombre qui revient le plus souvent. Le salaire modal est à 2000 € chez XYZ.

Cet exemple, nous amène à toujours nous interroger sur l’utilisation des mesures de tendance centrale, en se demandant laquelle est utilisé et comment ce choix se justifie.

Dans cette émission,, nous allons continuer avec l’étude de l’écart type et des sondages et échantillonnages qui fleurissent dans les médias en cette période électorale.

En plus des mesures de tendance centrale, la pensée critique doit nous amener à nous intéresser à la dispersion d’une distribution, soit l’étude des variations autour de la moyenne. Et la plus importante des mesures de cette dispersion est l’écart type.

Imaginons que vous avez été pêché dans une eau que l’on vous dit polluée, rendant impropre à la consommation un certains n ombres de poissons. On vous dit aussi que certains poissons sont sans danger. On va supposer que la toxicité des poissons se répartie selon une courbe normale. On vous apprend que l’usine de Spountz voisine a déversé en secret un produit toxique, le Cecicela, jusqu’à ce l’usine soit transformée en coopérative ouvrière autogérée. On vous dit qu’à partir de 7mg de Cecicela, il devient dangereux de manger un poisson. La moyenne des quantités de Cecicela retrouvées dans les poissons de ce cours d’eau est de 4mg. La question que vous vous posez est : allez-vous en manger ?

Avant de consommer ces poissons, vous feriez bien de vous renseigner sur l’écart type, pour savoir si les valeurs de toxicité varient peu autour de cette moyenne ou beaucoup. En clair si les valeurs varient beaucoup, vous prenez un grand risque d’avoir des poissons qui dépassent la toxicité critique de 7mg. Alors que si elles varient entre 3mg et 5mg, la moyenne est toujours de 4mg mais il y a peu de risque de dépasser la dose fatidique de 7mg !

Ainsi, l’écart type est une mesure de la dispersion statistique d’un ensemble de valeurs autour d’une valeur moyenne. Elle se calcule comme la racine carrée d’une autre valeur appelée la variance. On la nomme sigma ( ϭ ) et on note :

Ϭ égale racine carrée de la somme des xi moins la moyenne des x divisée par n, le nombre de valeurs.

Heureusement pour vous, il existe d’autres manières de calculer l’écart type.

La plus simple consiste à faire appel à une calculatrice, scientifique ou statistiques – comme il en existe sur vos ordinateurs personnels-, qui vous donnera l’écart type par simple pression de la touche adéquate, représentée souvent par un sigma.

Si vous devez faire le calcul manuellement voici les étapes à respecter.

1° calculez la moyenne de votre distribution

2° déterminez l’écart entre chacune de vos valeurs avec la moyenne précédemment calculée

3° prenez le carré de chacun de ces écarts

4° faites le total de tous ces carrés

5° divisez ce total par le nombre de valeurs, vous obtenez la variance

6° enfin prenez la racine carrée de cette variance pour obtenir votre écart type.

7° faites ouf

Dans la collection suivante de valeurs : 2, 2, 3, 5, 7, 9, 14 la moyenne est de 6,  la variance est de 16,57 et l’écart type de 4,07.

Il existe une troisième méthode qui donne une valeur très approximative mais utile à connaître car elle se calcule facilement et rapidement.

1° prenez la plus haute valeur de votre collection, puis soustrayez en la plus petite : vous obtenez l’intervalle de variation numérique de la collection, on l’appelle l’étendue ou la fourchette ;

2° Divisez ensuite le nombre obtenu par quatre. Mais rappelez-vous que ce résultat n’est qu’une très grossière approximation de l’écart type.

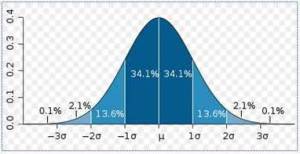
Cette mesure est extrêmement utile pour le calcul statistique, en particulier avec la moyenne, l’écart type nous donne beaucoup d’informations pour les collections qui suivent la loi normale, se répartissent selon une courbe de Gauss. Au milieu de votre courbe en chapeau se trouve la moyenne et de part et d’autres de cette moyenne, vous aurez 68,2% de vos valeurs réparties autour de la moyenne jusqu’à une fois l’écart type, quand vous aurez 95,4% de ces données se trouvant autour jusqu’à 2 fois l’écart type et enfin ce sont 99,8% des données qui sont comprises entre la moyenne moins 3 fois l’écart type et la moyenne plus 3 fois l’écart type, donc très peu sont au-delà de ces bornes (0,2%).

Vous pourrez trouver sur notre article en ligne une représentation de cette courbe :

Ainsi si la moyenne est de 12et l’écart- type de 3, environ 68,2% des valeurs de la collection seront comprises entre 9 et 15.

Revenons à l’exemple des poissons, si l’écart type est de 1mg, mangerez-vous des poissons péchés et s’il est de 4mg, que ferez-vous ? Rappelez-vous que la toxicité moyenne des poissons était de 4mg et le danger au-delà de 7mg. Dans le premier cas vous saurez que 98,8% des poissons auront un taux de toxicité compris entre 1mg et 7mg, donc un risque de 0,1% d’avoir des poissons avec une toxicité de plus de 7mg. Dans le deuxième cas, le risque est environ 200 fois plus grand.

Ainsi, on voit que la statistique permet de décrire des données mais aussi de les analyser.

Ces aspects nous intéressent particulièrement, avec d’autres outils pour l’étude des sondages et du jugement apporté sur les échantillonnages.

Lors de la prochaine émission, nous reviendrons sur l’importance de bien connaître ces mesures de tendance centrale et verrons comment les utiliser judicieusement. Enfin, n’oubliez pas les conseils des émissions précédentes, ces conseils vous sont donnés pour laisser le moins de prise possible à l’émotion manipulatrice voulue.

Et retrouvez sur le site du cercle libertaire jean-barrué (http://cerclelibertairejb33.free.fr ) nos chroniques en référence au « Petit cours d’autodéfense intellectuelle » de Normand Baillargeon.

Alors, à dans un mois.