Chronique raisonnable n° 19 ou leçon d’autodéfense intellectuelle du jeudi 3 mai 2012

19^ème chronique raisonnable, pour :

o     apprendre à soumettre à la critique les informations reçues

·        prévenir les manipulations et

·        démonter les croyances,

« Être libre, c’est ne plus avoir peur et être responsable de sa vie ».

Continuons ensemble l’étude des pièges d’un usage malicieux des mathématiques : apprendre à compter pour ne pas s’en laisser conter. Rappelez-vous l’émission précédente !

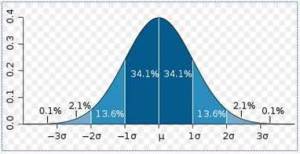
Nous avons vu un des outils de base de la statistique, avec l’écart type, qui est une mesure de la dispersion statistique d’un ensemble de valeurs autour d’une valeur moyenne. Associé à la moyenne, il permet de fournir une représentation suivant la courbe de Gauss Laplace, la courbe en chapeau, elle concerne la représentation de la distribution de nombreux phénomènes humains ou naturels qui suivent la loi dite « normale ». Dans cette courbe, les valeurs se répartissent autour de la moyenne, avec des pourcentages connus pour chaque tranche de la taille de l’écart type. Ci-dessous le dessin de cette courbe :

N’oublions pas que si la statistique permet de décrire des données, elle permet aussi de les analyser. Nous avons ainsi pu décider si nous allions manger ou non des poissons péchés dans une rivière polluée et dans quels cas.

Ces aspects nous intéressent particulièrement, avec d’autres outils pour l’étude des sondages et du jugement apporté sur les échantillonnages.

Dans cette émission,, nous allons continuer avec l’étude des sondages et échantillonnages qui ont fleuri dans les médias en cette période électorale.

La statistique permet de déduire les propriétés de toute une population à partir de l’étude d’une petite partie de cette population. Cette petite partie est appelée l’échantillon. Constituer des échantillons et les qualifier est une des applications importantes de la statistique. Et sa forme la plus popularisée est le sondage.

Lorsque les populations sont très grandes, connaître leurs propriétés est long et coûteux. Il s’agit sans passer par le recensement de connaître, malgré tout, certaines propriétés d’une population donnée.

Les exemples de question sont nombreux : l’intention de vote des électeurs d’un pays, sans avoir à réaliser le vote lui-même ni dépenser autant d’énergie, ou connaître le nombre de matraques défectueuses à la sortie de l’usine, sans avoir à les contrôler une à une. C’est grâce à la statistique que l’on pourra étendre le jugement sur un échantillon à un jugement sur l’ensemble du groupe étudié.

Mais l’exemple le plus enfantin d’échantillon est trouvé lorsque pour savoir si la soupe est trop ou pas assez chaude, nous goûtons une cuillerée du chaudron de soupe, à ce moment-là, nous jugeons sur un échantillon.

La constitution des échantillons est aussi complexe qu’essentielle pour la validité du jugement porté à partir de la statistique.

Pour que ce jugement soit valable, il faut que l’échantillon soit représentatif de la population que l’on étudie. Pour cela, l’échantillon devra être suffisamment grand et non biaisé. Ainsi si l’on reprend l’exemple du chaudron de soupe, si l’on teste une goutte de soupe, on peut penser que l’échantillon est trop petit, de même si l’on prend l’échantillon juste à l’endroit ou le cuisinier vient de poivrer la soupe sans remuer, là on peut penser que l’échantillon sera biaisé s’il s’agit de savoir s’il est trop ou pas assez poivré.

Il existe bien des exemples où l’échantillon est important et pour autant où les données que l’on en tire ne sont pas fiables, car l’échantillon aura été qualitativement biaisé. On raconte ainsi l’aventure de la revue américaine Literary Digest qui depuis 1920 réalisait des sondages lors de la tenue des élections présidentielles. Cette revue connut du succès dans ses prédictions. Elle organisait des « votes de paille », elle envoyait, avant la tenue des élections, de faux bulletins de vote où les personnes qui le désiraient indiquer le nom du candidat pour qui elles voteraient et renvoyer le bulletin. C’est de la comptabilisation de ces envois qu’était tirée la prédiction. Les résultats se sont avérés justes, puisque la revue annonçait le gagnant, mais imprécis car l’écart entre la prédiction et le résultat fluctua entre 0,9% et 44%. Entre 11 et 20 millions de bulletins étaient envoyés et il y eut jusqu’à 3 millions de réponses en retour.

Jusqu’en 1936, où la revue annonça la victoire du républicain Alfred Mossman Landon contre le démocrate Franklin D. Roosvelt.

Dans le même temps, un jeune psychologue, George Gallup, avait, en interrogeant 4 500 personnes, prédit l’élection de Franklin D. Roosvelt. Et c’est ce dernier qui l’emporta avec 60,8% des voix contre 36,6% pour l’adversaire républicain, soit l’une des plus importantes majorités de toutes les élections présidentielles américaines.

La raison de l’échec du Literary Digest ? Son échantillon, bien qu’énorme, était biaisé alors que celui de Gallup bien que considérablement plus petit ne l’était pas. Et Gallup devint le fondateur de la célèbre agence de sondages. La revue choisissait les gens à qui elle envoyait ses bulletins de paille parmi ses abonnés et des personnes prises au hasard dans l’annuaire téléphonique. Ainsi, elle sur-sélectionnait des gens plus fortunés et plus enclin à voter républicain, puisqu’ils avaient choisi de s’abonner à cette revue plutôt conservatrice ou qu’ils avaient les moyens de se payer un abonnement téléphonique dans les années 30.

On peut donc retenir qu’un bon échantillon représentatif d’une population doit être suffisamment grand (vertu quantitative) et non biaisé (vertu qualitative).

Quelle est la taille d’un bon échantillon ? C’est une question complexe et l’on peut retenir que la plupart des sondages d’opinion portent sur un échantillon de 1 000 à 2 000 personnes. Ce que l’on peut dire c’est que la recherche d’une nouvelle précision obtenue par une population plus grande coûterait beaucoup trop cher.

Pour obtenir un échantillon non biaisé, il faut s’attarder sur le processus de la sélection : on doit choisir au hasard les individus qui en feront partie. Chaque élément doit avoir la même chance que n’importe quel autre d’être choisi et le fait qu’un élément soit retenu, ne doit avoir aucune incidence sur la sélection des autres. Comme cet idéal théorique est difficile à réaliser en pratique, des méthodes d’échantillonnage ont été développées, mais à chaque fois les éléments de l’échantillon doivent être sélectionnés au hasard. C’est le respect de ce principe qui va garantir que les analyses portées sur l’échantillon peuvent être généralisées à toute la population.

Ce principe est donc indispensable à la connaissance du penseur critique, qui doit pouvoir juger instinctivement des échantillons.

Prenons quelques exemples :

1 – une station de radio fait un sondage sur la légalisation de la consommation de cannabis. Sur une population de 3 636 auditeurs, 78% ont répondu favorablement à cette légalisation. Et la radio en conclut que c’est l’heure de légaliser la marijuana. Mais l’échantillon n’a pas été constitué au hasard puisqu’il est constitué des auditeurs de la radio et que ceux qui ont répondu sont ceux qui étaient motivés pour le faire. Rien ne peut donc être conclut de ce sondage.

2 – Un sondage Gallup concluait que 33% des personnes ayant fréquenté l’université ne connaissaient pas le système métrique. Alors qu’un sondage mené par un quotidien californien établissait que 98% de ses lecteurs le connaissaient. La méthode consista à faire remplir un bulletin par les lecteurs du journal, puis à le faire découper et renvoyer par les lecteurs eux-mêmes. Donc, on peut penser que le sondage du journal est biaisé car les personnes ne connaissant pas le système métrique s’en sont autoexclues.

Lors de la prochaine émission, verrons comment distinguer corrélation statistique et causalité de deux évènements. Enfin, n’oubliez pas les conseils des émissions précédentes, ces conseils vous sont donnés pour laisser le moins de prise possible à l’émotion manipulatrice voulue.

Et retrouvez sur le site du cercle libertaire jean-barrué (http://cerclelibertairejb33.free.fr ) nos chroniques en référence au « Petit cours d’autodéfense intellectuelle » de Normand Baillargeon.

Alors, à dans quinze jours.